Abstract:
An algorithm for combined numerical and symbolic analysis of the time domain network function is proposed. This algorithm is useful in these cases, when circuit parameters are given numerically, but some are symbols in the network function. One of these cases is repetitive analysis, where the same network function is calcutaled many times by substituting symbol variables by numerical values. Advanced techniques used in repetitive frequency analysis were implemented in time domain analysis by utilising polynomial number method.
Streszczenie:
W pracy zaproponowano algorytm obliczania funkcji sieci w dziedzinie czasowej dla przypadku kiedy część parametrów sieci zadana jest jawnie w postaci numerycznej, a część (kilka do kilkunastu) w postaci symbolicznej. Algorytm jest użyteczny w czasowej analizie wielowariantowej, to jest w przypadku, gdy trzeba generować dużą ilość charakterystyk przy wielu wariantach danych podstawianych za zmienne symboliczne. Poprzez wykorzystanie rachunku liczb wielomianowych możliwe było przeniesienie do obliczeń czasowych zaawansowanych metod stosowanych w dziedzinie częstotliwości.
1. Wstęp
Jednym z zastosowań symbolicznej analizy funkcji (transmitancji) obwodu są obliczenia numeryczne wykorzystujące wcześniej wygenerowane i odpowiednio przetworzone wzory, dzięki czemu wielokrotnie wykonywane obliczenia wykonywane są szybciej i dokładniej. Podczas tych obliczeń cześć parametrów obwodu przyjmuje ustalone numeryczne wartości, a część reprezentowana jest przez zmienne symboliczne, co pozwala po odpowiednich przekształceniach utworzyć wzór, gdzie obok zmiennych symbolicznych występują współczynniki liczbowe. Funkcja sieci ma postać funkcji wymiernej, w której liczniku i mianowniku występują wielomiany zmiennych symbolicznych y1, y2, ...yM [1]:
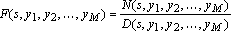 |
(1) |
Wzór funkcji sieci obliczany jest najczęściej w dziedzinie transformat Laplce'a, stąd pojawia się zmienna zespolona s, która podczas obliczeń numerycznych przyjmuje wartości s = jwk przy analizie AC lub s = 0 przy analizie DC. Można znacząco usprawnić proces obliczeń wielowariantowych w dziedzinie częstotliwości, poprzez podstawienie za s we wzorze (1) kolejnych wartości jwk i dalsze ich przekształcenie, tak, że w pętli wielokrotnych obliczeń, występują funkcje, których argumentami są już wyłącznie zmienne symboliczne [2, 3]. W jednym punkcie częstotliwości wk mamy więc
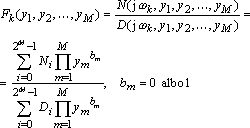 |
(2) |
Wielomiany w liczniku i mianowniku funkcji sieci, nazwane bilinomami, uzyskują wtedy możliwie najprostszą postać, gdzie obok współczynników liczbowych Ni , Di występują iloczyny zmiennych symbolicznych w potędze 0 lub 1. Wykładnik bm jest m-tym bitem rozwinięcia dwójkowego liczby i.
Dla każdej częstotliwości wk generowany jest wzór (2), a potem dopiero całą rodzinę wzorów wykorzystuje się w pętli analizy wielowariantowej. Wartości współczynników liczbowych w (2) zależą od parametrów obwodu danych numerycznie i od układu połączeń, ale czas obliczeń dla kolejnych wariantów y1, y2, ...yM nie zależy już od złożoności obwodu, a jedynie od ilości zmiennych symbolicznych i ilości punktów częstotliwości. Uzyskane przyśpieszenie obliczeń jest w tym przypadku okupione dużym zapotrzebowaniem na pamięć komputera dla pamiętania wszystkich współczynników dla całej rodziny wzorów.
Szybkie obliczenia charakterystyk częstotliwościowych mogą być podstawą do wyznaczania charakterystyk czasowych układu (np. odpowiedzi skokowej układu) poprzez użycie odwrotnego przekształcenia Fouriera (FFT) [4]. W takim jednak przypadku nie można uwzględniać niezerowych warunków początkowych, dodatkowo mamy do czynienia z błędem aliasingu, gdyż sygnały mają widma nieograniczone.
Wad tych pozbawiony jest sposób zaproponowany w [5], gdzie zastosowano technikę zamiany każdego elementu rektancyjnego w obwodzie odpowiednim dwójnikiem modelującym równania różnicowe wynikające z różniczkowania czy całkowania numerycznego, a następnie stosowanie do tak przetworzonego obwodu algorytmów analizy symbolicznej. Gdyby chcieć zastosować tę metodę do analizy wielowariantowej, to jej wadą byłby rosnący czas obliczeń przy rosnącej złożoności obwodu ([5], tab. 1 na str. 32).
Połączenie wspomnianej wcześniej metody bilinomów i metody liczb wielomianowych [6, 7] pozwala w analizie wielowariantowej charakterystyk czasowych na osiągnięcie czasu analizy niezależnego od złożoności obwodu.
2. Liczby wielomianowe
Metoda liczb wielomianowych [7] jest kontynuacją metody operatorów liczbowych Bellerta [8], która była adaptacją koncepcji rachunku operatorów Mikusińskiego w dziedzinę równań różnicowych
Liczba wielomianowa jest to uogólniona liczba, której cyfry są elementami pewnego ciała, na przykład ciała liczb rzeczywistych. Pełni ona w analizie stanów nieustalonych tę samą rolę co liczba zespolona w przypadku przebiegów sinusoidalnych. Liczby takie mogą być związane wzajemnie jednoznacznie z funkcjami lub ciągami (rys. 1). Ich podobieństwo do liczb rzeczywistych pozwala na zaprogramowanie algorytmów działań wzorowanych na algorytmach zmiennoprzecinkowych dla liczb binarnych. Prowadzi to do wspomaganego komputerowo rachunku operatorowego, pozwalającego zarówno na prowadzenie na komputerze działań w dziedzinie transformat, jak i automatyczne wyznaczanie transformaty odwrotnej w postaci ciągu próbek rozwiązania, czy ciągu współczynników szeregu opisującego rozwiązanie.
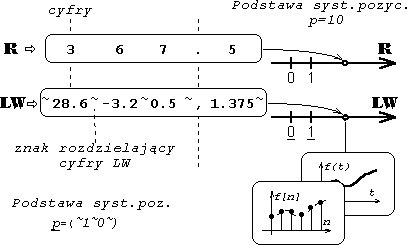
Rys. 1. Porównanie liczby rzeczywistej dziesiętnej i liczby wielomianowej.
Podobieństwo podstawowych działań dla liczb wielomianowych i liczb rzeczywistych dzisiętnych czy binarnych jest daleko idące, a główną różnicą jest to, że w operacji dodawania (odejmowania) nie występuje przepełnienie (pożyczka) przy operacji na cyfrach. Analogicznie do liczb binarnych liczby wielomianowe są w komputerze pamiętane jako para mantysa - cecha, przy czym mantysa jest ucięta do z góry ustalonej ilości N cyfr (np. N = 128). Liczba wielomianowa może być wzajemnie jednoznacznie powiązana z funkcją lub ciągiem liczb, a więc także z transformatą Laplace'a F(s) lub Z transformatą F(z) sygnału czy transmitancji obwodu. Dalej ograniczymy rozważania do związku liczb wielomianowych z transformatą Z.
Tabela 1 pokazuje przykłady transformat Z i ich odpowiedniki w dziedzinie liczb wielomianowych. Liczba wielomianowa odpowiadająca sygnałowi e(t) składa się z cyfr, które są kolejnymi próbkami sygnału: e(0), e(h), e(2h) , e(3h), ... , gdzie h jest krokiem próbkowania. Zauważmy, że ucięcie mantysy liczby wielomianowej do N cyfr znaczących oznacza, że przedział czasowy rozwiązania będzie ograniczony do czasu od 0 do (N-1)h. Liczby wielomianowe odpowiadające impedancji cewki lub admitancji kondensatora mają wartość ZL = p L, YC = p C, gdzie p jest stałą liczbą wielomianową zależną od wybranej metody różniczkowania lub całkowania numerycznego. Podobnie jak w przypadku metody liczb zespolonych, każdemu sygnałowi i każdej transmitancji obwodu odpowiada wzajemnie jednoznacznie jedna liczba. Mając oprogramowane wszystkie działania podstawowe dla liczb wielomianowych można posługiwać się nimi w odniesieniu do sygnałów dowolnych analogicznie jak posługujemy się liczbami zespolonymi w odniesieniu do sygnałów sinusoidalnych.
Tabela 1
|
Transformata Z (h - krok próbkowania) |
Odpowiadająca jej liczba wielomianowa |
|
Zmienna zespolona z |
Podstawa systemu (~ 1 ~ 0 ~) |
|
1. Ciąg próbek { e(0), e(h), e(2h) , e(3h), ...} |
|
|
e(0) z0 + e(h) z-1 + e(2h) z-2 + e(3h) z-3 + ... |
(~ e(0) ~, e(h) ~ e(2h) ~ e(3h) ~ ... ~) |
|
2. Odwrotność operatora przybliżonego całkowania (alg. trapezów) |
|
|
p(z) = 2/h (1-z-1) / ( 1+z-1) |
p = 2/h (~ 1 ~, -1 ~)/(~ 1 ~, 1 ~) = 2/h (~ 1 ~, -2 ~ 2 ~ -2 ~ 2 ~... ~) |
3. Proces obliczeniowy
Obliczenia wielowariantowe charakterystyki czasowej z wykorzystaniem liczb wielomianowych mogą przebiegać następująco:
Punktem wyjściowym niech będzie transformata Laplace'a F(s, y) poszukiwanej charakterystyki obwodu (np. odpowiedzi skokowej) w postaci (1), gdzie wybrane parametry obwodu opisane są symbolicznie. Po podstawieniu ([7]) za zmienną s liczby wielomianowej p odpowiadającej odwrotności operatora przybliżonego całkowania i przemnożeniu transformaty przez p / (~1~, -1~) dostaje się wzór dla liczby wielomianowej, która jest transformatą Z poszukiwanej charakterystyki. Dla przykładu z dwoma zmiennymi symbolicznymi wyznaczane są kolejno następujące wyrażenia:
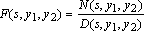 |
(3) |
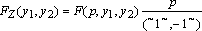 |
(4) |
po czym przekształca się (4) do postaci z bilinomami w liczniku i mianowniku jak w (2), to jest
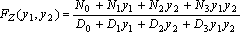 |
(5) |
Następnie w pętli podstawiane są kolejne warianty wartości dla zmiennych symbolicznych i na podstawie (5) uzyskiwane są liczby wielomianowe, których cyfry są ciągiem próbek analizowanej funkcji czasowej.
Tak więc przed pętlą wariantów przygotowuje się jeden wzór (5), a nie K wzorów jak przy analizie w K punktach częstotliwości, z tym, że nadal zapotrzebowanie na pamięć komputera jest znaczące, gdyż każdy współczynnik - liczba wielomianowa N0 .. N3 , D0 .. D3 zawiera w sobie ciąg N liczb rzeczywistych (gdzie N to ilość próbek czasowych analizowanej charakterystyki). Warto przy tym dodać, że użycie liczb wielomianowych pozwala uwzględniać elementy obwodu o parametrach rozłożonych [7].
4. Eksperymenty numeryczne
Wyznaczanie wartości liczy wielomianowej według wzoru (5) wymaga przeprowadzenia 6 operacji skalowania (mnożenia liczby wielomianowej przez liczbę rzeczywistą), sześciu operacji dodawania i jednego dzielenia liczb wielomianowych. Ta ostatnia operacja jest najbardziej czasochłonna. Jej asymptotyczna złożoność czasowa jest rzędu takiego jak dla obliczanie splotu cyfrowego.
Zaproponowany wyżej algorytm testowano dla różnych układów przy różnej ilości próbek czasowych. Całkowity czas obliczeń jednego wariantu dla liczb wielomianowych 64-cyfrowych przy dwóch zmiennych symbolicznych wynosi 4.2ms (procesor Pentium, 130MHz), dla 128 próbek czas wynosi 15ms/wariant. Dla dużej ilości próbek czasowa złożoność obliczeniowa jest rzędu takiego jak złożoność algorytmu FFT. Należy tu podkreślić, że przy proponowanym algorytmie czas analizy jednego wariantu nie zależy od skali skomplikowania analizowanego obwodu.
5. Podsumowanie
Zaproponowany w tym artykule algorytm wielowariantowej analizy funkcji sieci w dziedzinie czasu jest połączeniem metody generowania wzorów opartych na bilinomach, stosowanych w analizie częstotliwościowej oraz metody liczb wielomianowych, która jest komputerowym rachunkiem operatorowym. Uzyskuje się przez to w dziedzinie czasu szybkie obliczenia funkcji analizowanego obwodu i to niezależnie od stopnia jego złożoności, dzięki rozdzieleniu procesu na dwa etapy. W pierwszym następuje przygotowanie wzorów numeryczno symbolicznych, przy czym współczynniki numeryczne są liczbami wielomianowymi. W drugim etapie następują wielokrotnie powtarzane obliczenia analizowanej funkcji sieci przy różnych wariantach danych liczbowych podstawianych za wielkości symboliczne. W tym etapie przy ustalonej ilości próbek analizowanej funkcji i ilości zmiennych symbolicznych szybkość obliczeń zależy wyłącznie od sprawności algorytmów działań na liczbach wielomianowych. Metoda ma swoje ograniczenia, jak np. stały krok próbkowania funkcji czasowych czy ograniczony na wstępnie zakres czasu, dla którego wykonywana jest analiza. Jednak duża szybkość obliczeń tym sposobem pozwala mieć nadzieję, że metoda znajdzie zastosowanie w praktyce.
6. Literatura
[1] Lin, P.M., "Symbolic Network Analysis",- Elsevier, Amsterdam. 1991
[2] Dmytryshyn, R.V., "The Use of Symbolic-Numerical Methods for Electronic Circuit Analysis", Proc. of ISCAS'93 , Chicago, USA ,1993, pp. 1655-1657
[3] Dmytryshyn, R., "Metody wielomianowe analizy symbolicznej obwodów elektrycznych", Rozprawa hab., Politechnika Lwowska, Ukraina, 1996, s.284, (w języku ukraińskim)
[4] Hassoun, M., Ackerman, E., "Symbolic simulation of large-scale circuits in both frequency and time domain", Proc. of 33th MWSCAS, USA, 1990, pp. 707-710.
[5] Greenfield, S.E.; Hassoun, M.M., " Direct hierarchical symbolic transient analysis of linear circuits ", IEEE Intern. Symp. on CaS, New York, USA, 1994, pp 29-32.
[6] Kubaszek, A., "The Polynomial Number Method for Computation Signal Waveforms in Frequency Dependent Parameter Interconnection Lines", ECCTD-91, Kopenhaga 1991., pp. 709-718..
[7] Kubaszek, A., "Komputerowa analiza propagacji sygnałów metodą liczb wielomianowych", Rozprawa doktorska, Politechnika Poznańska, Poznań 1994, s. 101.
[8] Bellert, S., "Metoda operatorów liczbowych", Rozprawy Elektrotechniczne ,t.1, zesz. 4, 1959.
| dr inż. Andrzej Kubaszek |
| Politechnika Rzeszowska, |
| Zakład Elektrotechniki Teoretycznej, |
| ul. W. Pola 2, |
| 35-959 RZESZÓW |
| kubaszek@prz.edu.pl |