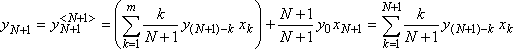Andrzej Kubaszek
Liczby wielomianowe - algorytmy działań
1. WSTĘP
Liczby wielomianowe rzeczywiste [1, 2, 3] są prostym rozszerzeniem tradycyjnych liczb rzeczywistych - polega ono na zniesieniu ograniczeń na cyfry rozwinięcia potęgowego liczby tak, że zamiast należeć do skończonego zbioru liczb całkowitych (np. 0..9) należą one do jakiegoś ciała np. liczb rzeczywistych czy zespolonych. Arytmetyka takich uogólnionych liczb jest podobna do arytmetyki liczb tradycyjnych z jednym wyjątkiem - przy dodawaniu nie występują przeniesienia. W tej sytuacji nieważna staje się wartość podstawy (zasady) liczby, która pełni już tylko rolę operatora zmiany pozycji cyfr (tę samą rolę pełni rówież podstawa liczb tradycyjnych).
Arytmetyka liczb wielomianowych daje się łatwo zaimplementować na komputerze dzięki wykorzystaniu bogatych doświadczeń z arytmetyką tradycyjnych liczb rzeczywistych (np. arytmetyka zmiennoprzecinkowa), liczby te natomiast są odpowiednikiem funkcji jednej zmiennej (dowolnej np. zespolonej), pozwalają więc na prowadzenie rachunku Laplace'a czy Z na komputerze (wszelkie działania w dziedzinie transformat, obliczanie retransformaty). Procedury działań na liczbach wielomianowych można udostępnić w postaci języka symulacyjnego, czyli wysokiej klasy kalkulatora łatwego w obsłudze - ciekawa jest tu analogia: kalkulator inżynierski spowodował drastyczne ograniczenie zastosowania tablic podstawowych funkcji matematycznych, kalkulator liczb wielomianowych miałby szansę istotnego ograniczenia zastosowania tablic transformat.
Do tej pory przydatność idei liczb wielomianowych wypróbowałem przy analizie obwodów skupionych metodą przekształcenia Z i Laplace'a [1], oraz przy analizie linii długiej stratnej dowolnie obciążonej [2], z uwzględnieniem zjawiska wypierania prądu przy większych częstotliwościach (naskórkowość) [3] z wykorzystaniem przekształcenia Laplace'a. Końcowym efektem tej analizy są wykresy wybranych przebiegów czasowych (rys.1). W [3] pokazałem też proste przykłady odtwarzania obwodu elektrycznego na podstawie jego zespolonej charakerystyki widmowej wykorzystując transmitancję obwodu w dziedzinie liczb wielomianowych. Zebrane dotąd doświadczenia przekonują mnie, że idea liczb wielomianowych inspiruje myślenie o złożonych problemach innymi, może prostszymi i dobrze znanymi każdemu kategoriami, ma więc dużą wartość dydaktyczną, oraz że pomimo prostoty otwiera ona ciekawe pole problemów.
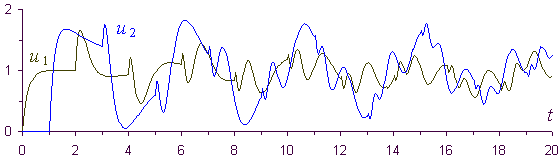
Rys. 1. Przebiegi czasowe napięć na (początku i) końcu
linii długiej stratnej po załączeniu poprzez cewkę napięcia stałego i przy
obciążeniu jej odbiornikiem R, L
W tej pracy formalnie opiszę podstawowe działania na liczbach wielomianowych, dalej wspomnę o znanych szybkich algorytmach mnożenia i odwracania oraz pokażę jeszcze szybsze i dokładniejsze algorytmy obliczania odwrotności i pierwiastka kwadratowego liczby. Na koniec podam efektywne algorytmy obliczania podstawowych funkcji matematycznych jak ex, sin x, xa, ln x.
2. PODSTAWOWE DZIAŁANIA
Rozwinięcie potęgowe liczby wielomianowej a o cyfrach aj i podstawie p wygodnie jest przedstawiać w zapisie pozycyjnym (znaku "~" używam dla wyraźnego rozdzielenia cyfr, oznaczenia liczb wielomianowych będę podkreślał):
a = 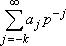 = (~a-k~...~a-1~a0~, a1~a2~...~)p . = (~a-k~...~a-1~a0~, a1~a2~...~)p .
|
(1) |
Oznaczenie podstawy p = 1 p+0 = (~1~0~) będzie najczęściej pomijane (podobnie jak przy zapisie liczb tradycyjnych).
Przykład:
| 5.6 p2- 9 + 7.88 p-1+ 15.6 p-3= (~5.6~0~-9~, 7.88~0~15.6~). |
W obliczeniach komputerowych można używać arytmetyki zmiennoprzecinkowej, dzięki której działania na liczbach rzeczywistych sprowadzane są praktycznie do działań na liczbach całkowitych. Liczba wielomianowa całkowita (bez części po przecinku) jest odpowiednikiem wielomianu, dla którego podstawowe działania są każdemu dobrze znane. W poniżej prezentowanych wzorach będę używał notacji związanej z tą arytmetyką - liczba będzie opisywana mantysą z jedną cyfrą przed przecinkiem i cechą, przy czym pierwsza cyfra mantysy nie zawsze musi być różna od 0. Niech
|
a = (~a0~, a1~a2~...~) (~1~0~)m
b = (~b0~, b1~b2~...~) (~1~0~)m |
| a + b = c = (~c0~, c1~c2~...~) (~1~0~)m, cj= aj+ bj , | (2) |
| s a = (~s a0~, s a1~s a2~...~) (~1~0~)m , | (3) |
gdzie j = 0,1,..., zaś s - liczba tradycyjna. Niech przy b0 ≠ 0
|
a = (~a0~, a1~a2~...~) (~1~0~)m,
b = (~b0~, b1~b2~...~) (~1~0~)n |
a ∙ b =
c = (~c0~, c1~c2~...~)∙(~1~0~)m+n , cj=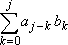 , ,
|
(4) |
a / b = d = (~d0~, d1~...~)∙(~1~0~)m-n,
dj =
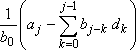 ,
j = 0,1,... ,
j = 0,1,...
|
(5) |
Jeżeli cyframi liczby wielomianowej są liczby rzeczywiste, to można mówić o uogólnieniu liczb tradycyjnych w podwójnym sensie. Po pierwsze liczba wielomianowa jednocyfrowa z jedną cyfrą przed przecinkiem (pozostałe są zerowe) jest rownoważna liczbie tradycyjnej: (~x0~)=x0. Po drugie liczby tradycyjne i wielomianowe o takich samych cyfrach i podstawach wskazują tę samą wartość np.:
| (~1~8~, 7~2~)10= 1∙10 +8 +7∙10-1+2∙10-2= 18.72 | (6) |
Ze względu na brak przeniesień reguły dodawania liczb wielomianowych są jednak inne niż dodawania liczb tradycyjnych np.:
| (~1~8~, 7~2~)10+(~5~, 4~)10= (~1~13~, 11~2~)10= 24.12 , | (7) |
oczywiście także 18.72 +5.4 = 24.12 .
3. SZYBKIE MNOŻENIE, ODWRACANIE I PIERWIASTKOWANIE
Na początek zauważmy, że mantysę iloczynu dwóch liczb wielomianowych (4) można szybko obliczyć algorytmem FFT, czyli mnożenie może być wspomagane szybkim procesorem sprzętowym realizującym FFT. Z kolei mając szybką operację mnożenia można podać bardzo efektywny algorym odwaracania, podwajający w każdym kroku liczbę cyfr dokładnych wyniku. Opiera się on na następującym rozumowaniu (podaję za [4]): jeżeli A ≈ x-1jest przybliżeniem odwrotności x to
| x-1= A + (x-1-A) = A + x-1(1-A x) |
Gdy A jest "dobrym" przybliżeniem to drugi składnik wyrażenia jest "mały", stąd zastąpienie tam x-1 przez A da algorytm coraz lepszych przybliżeń:
| A<K+1>= A<K>+ A<K>( (~1~) - A<K>x ) = 2 A<K>+ (A<K>)2x , | (8) |
gdzie A<K>jest K-tym przybliżeniem x-1. W przypadku liczb wielomianowych można ten algorytm udoskonalić. Algorytm dotyczy mantysy liczby, a więc x = (~x0~, x1~x2~...~). Dokładnie znana jest pierwsza cyfra x-1(na podstawie (4)), przyjmijmy ją za pierwsze przybliżenie odwrotności:
| A<0>= x0-1 |
Dalej załóżmy, że w k-tym przybliżeniu A<K>mamy n początkowych cyfr dokładnych (takich samych jak w x-1), a dalsze są wyzerowane. Ponieważ przy dodawaniu i mnożeniu cyfra k-ta wyniku nie zależy od cyfr k+1 i dalszych argumentów, więc A<K>x = (~1~, 0~...~) z dokładnościa do n cyfr, stąd
|
r = A<K>( (~1~) - A<K>x) =
= A<K>( (~1~) - (~1~, 0~0~...~0~-cn~-cn+1~-cn+2~...~) = = A<K>(~0~, 0~0~...~0~cn~cn+1~cn+2~...~) |
(9) |
gdzie cm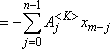 , m = n, n+1, ... (górna granica sumy
nie jest m, bo Aj<K>= 0 dla j ≥ n).
Z (8) i (9) mamy
, m = n, n+1, ... (górna granica sumy
nie jest m, bo Aj<K>= 0 dla j ≥ n).
Z (8) i (9) mamy
|
10) Aj<K+1>=
Aj<K>dla j = 0, ...,n-1
20) Am<K+1> 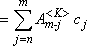 dla m =
n, n+1, ..., 2n-1 dla m =
n, n+1, ..., 2n-1
|
(10) |
Przybliżenie A<K+1>ma 2n cyfr dokładnie równych 2n najbardziej znaczącym cyfrom x-1, zaś obliczenie A<K+1>wymaga obliczenia tylko n cyfr An<K+1>.. A2<nK-+11>zamiast liczenia 2n cyfr algorytmem (8). Korzyść z tego jest podwójna - dostajemy algorytm działający szybciej i cyfry są obliczane dokładniej (wyeliminowanie zbędnych operacji), jeżeli obliczenia na cyfrach są prowadzone ze skończoną precyzją. Tabela 1 pokazuje co dziesiątą cyfrę pewnego argumentu x, jego odwrotność została obliczona dwoma algorytmami, wynikającymi z wzoru (8) i (10), cyfry były liczbami rzeczywistymi typu extended (około 19 cyfr dziesiętnych znaczących), mnożenie wykonywano wolnym algorytmem (4) w celu uniknięcia niwielkiego szumu wnoszonego przez algorytm FFT. Przy precyzji uwidocznionej w tabelce nie widać różnicy między dwoma wynikami, natomiast widać ją wyraźnie po ponownym pomnożeniu odwrotności przez argument. Wynik dokładny to (~1~, 0~0~...~), tabela pokazuje wyższość algorytmu (10) nad algorytmem (8).
| x * 1/x , 1/x obliczono | ||||
|---|---|---|---|---|
| cyfra | x | 1/x | algorytmem (8) | algorytmem (10) |
| 0: | 1.00 | 1.0000 | 1.000E+0000 | 1.000E+0000 |
| 10: | 1.30 | 0.0035 | 1.084E-0019 | 0.000E+0000 |
| 20: | 1.21 | 0.0051 | 6.505E-0019 | 0.000E+0000 |
| 30: | 0.32 | 0.0075 | 1.491E-0018 | -2.711E-0020 |
| 40: | -1.83 | 0.0110 | 9.758E-0019 | 0.000E+0000 |
| 50: | -5.45 | 0.0160 | -8.674E-0019 | 0.000E+0000 |
| 60: | -10.22 | 0.0234 | -8.674E-0018 | 0.000E+0000 |
| 70: | -14.74 | 0.0342 | -1.648E-0017 | 0.000E+0000 |
| 80: | -16.09 | 0.0499 | -2.082E-0017 | 0.000E+0000 |
| 90: | -9.76 | 0.0728 | -2.082E-0017 | 0.000E+0000 |
| 100: | 9.70 | 0.1064 | 8.674E-0018 | 0.000E+0000 |
| 110: | 46.61 | 0.1553 | 1.041E-0016 | 0.000E+0000 |
| 120: | 100.32 | 0.2268 | 2.429E-0016 | 0.000E+0000 |
| czas odwracania: | 6.65 sek. | 2.25 sek. | ||
Opierając się na podobnym
rozumowaniu można uzyskać algorytm dla A =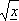 :
:
A<0>= 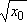 , A<K+1>=
0.5 (A<K>+ x
/ A<K>) , , A<K+1>=
0.5 (A<K>+ x
/ A<K>) ,
|
(11) |
który również podwaja w każdym kroku ilość cyfr dokładnych i który również można przyśpieszyć pdobnie jak algorytm odwracania.
4. ELEMENTARNE FUNKCJE LICZB WIELOMIANOWYCH
Wprowadzenie funkcji elementarnych pokażę na przykładzie ex. Zacznę od pomocniczej definicji pozwalającej na porównywanie liczb.
Def.: Rzędem liczby x (ozn. rank x) nazwiemy jej cechę przy mantysie z jedną niezerową cyfrą przed przecinkiem. Dodatkowo zakłada się, że rank (~0~) = 0. Rząd liczby jest więc ilością istotnych cyfr liczby przed przecinkiem pomniejszoną o 1.
Definicję ex wprowadzę w oparciu o szereg potęgowy.
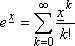 ,
x : rank x ≤ 0 , ,
x : rank x ≤ 0 ,
|
(12) |
czyli x = (~x0~, x1~x2~...~). Dziedzina funkcji jest ograniczona, gdyż dla argumentu x takiego, że rank x > 0 dostawałoby się wartość o nieskończonej ilości cyfr przed przecinkiem (rank ex = ∞), czyli obiekt nie będący liczbą wielomianową. Na marginesie trzeba tu wspomnieć, że w praktyce występuje potrzeba liczenia ex dla argumentu, którego rząd jest większy od zera, ale można go rozbić na dwa składniki x = x<1>+x<0>, gdzie rząd x<0> jest zerowy, co pozwala obliczyć ex<0>, natomiast ex<1> ma jakąś oddzielną interpretację np. może oznaczać opóźnienie w dziedzinie czasu sygnału obliczonego na podstawie ex<0> (tak powstał rys. 1).
Efektywny algorytm obliczania ex:
Niech ex = y = (~y0~, y1~y2~...~), x = (~x0~, x1~x2~...~). Wtedy
y0= ex0,
ym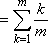 ym-k xk, m = 1, 2, ... ym-k xk, m = 1, 2, ...
|
(13) |
Uzasadnienie:
Na początek trzeba zauważyć, że e(~x0~) = ex0. Niech y<N>= e(~x0~, x1~...~xN~) będzie wartością funkcji dla argumentu uciętego do N cyfr po przecinku. Najbadziej znaczące cyfry y<N+1> do N-tej włącznie będą identyczne jak w y<N> bo:
y<N+1>=
e(~x0~, x1~...~xN~)
exN+1
(~1~0~)-(N+1)
=
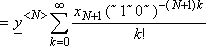 = =
= y<N>(1+ xN+1 (~1~0~)-(N+1)/1! +...) , |
(14) |
natomiast cyfra N+1 y<N+1>jest równa
| yN<+N1+1>= yN<+N1>+ y0<N>xN+1 | (15) |
Wiemy już, że yj<N+1>= yj dla j = 1, 2, ..., N+1. Załóżmy teraz prawdziwość twierdzenia dla N początkowych cyfr wyniku czyli, że
ym=
ym<N>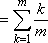 ym-kxk
, m =1,2,...,N , ym-kxk
, m =1,2,...,N ,
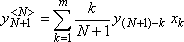
|
Wówczas
|
|
Czyli z poprawności algorytmu dla N najbardziej znaczących cyfr y wynika poprawność dla cyfry N+1.
Wzór algorymu wziąłem z [5], str. 181. Wzory tam podane dotyczą współczynników Taylora funkcji złożonej ex(t) i są związane z pewną metodą rozwiązywania równań różniczkowych (nieliniowych). Oto inne wzory przetransponowane z [5]:
ln y
= x
Þ
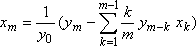
|
cos x
= c , sin x = s Þ
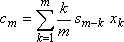 , ,
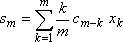
|
xa= y Þ 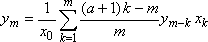
|
Zastosowanie tych wzorów wymaga umiejętności obliczenia pierwszej cyfry wyniku. W wypadku gdy argument funkcji jest liczbą, której rząd jest nie większy niż 0, można skorzystać ze znajomości tradycyjnej funkcji dla pierwszej cyfry przed przecinkiem.Powyższe algorytmy są w praktyce zadowalająco szybkie w przeciwieństwie do algorytmów opartych o rozwijanie w szereg. Na przykład przy mantysie 128 cyfrowej obiczanie ex trwało 153.7 sek. przy algorymie związanym z (12) i tylko 2.6 sek. przy algorytmie (13)! Dla większych mantys rożnice są jeszcze bardziej drastyczne.
5. ZAKOŃCZENIE I SPIS LITERATURY
Działania na liczbach wielomianowych są właściwie prostsze niż działania na liczbach tradycyjnych, stąd algorytmy stosowane dla liczb tradycyjnych można udoskonalić, uzyskując duże przyśpieszenie w przypadku obliczeń na liczbach wielomianowych. Pokazane w [1], [2], [3] zastosowania rachunku liczb wielomianowych pokazują, żepomimo wielu możliwych sposobów powiązania tych liczb z funkcjami f: R → R (wynikających np. z przekształcenia Laplacea czy Z) stosuje się te same, standardowe algorytmy warto je więc udoskonalać, a w końcu zrealizować sprzętowo.
- A. KUBASZEK: Liczby wielomianowe w analizie obwodów elektrycznych w stanie nieustalonym. Referat na XII SPETO, Gliwice - Wisła 1989.
- A. KUBASZEK: Metoda liczb wielomianowych w analizie stanu nieustalonego linii długiej stratnej. Referat na XII KKTOiUE, Rzeszów - Myczkowce 1989.
- A. KUBASZEK: Analiza stanu nieustalonego linii długiej metodą liczb wielomianowych z uwzględnieniem złożonej zależności parametrów linii od częstotliwości. Refeat zgłoszony na XII SPETO, Gliwice - Wisła 1990.
- A.V. AHO, J.E. HOPCROFT, J.D. ULMAN, Projektowanie algorytmów komputerowych. PWN, 1983.
- A. RALSTON, Wstęp do analizy numerycznej. PWN, 1983.
Andrzej KUBASZEK
Department of Electrical
Enginieering, I. Łukasiewicz
Technical University,
PL-35-959 Rzeszów, Poland.
Polynomial numbers - operation algorithms
Fast algorithms for operations with polynomial number (i.e. generalized numbers with digits from any field, for example real number field, and any variable as base) are presented in the paper. The numbers are used in the computer analysis of the differential and difference equations, by full analogy of the operations with traditional number operations (floating - point arithmetic). The presented algorithms are used in linear circuit analysis and the analysis of the lossy transmission line.
Liczby wielomianowe - algorytmy działań
W artykule zaprezentowano szybkie algorytmy działań na liczbach wielomianowych - są to uogólnione liczby, których cyfry należą do ciała np. liczb rzeczywistych, a podstawa (zasada) jest pewną zmienną. Liczby te pozwalają na algebraizację równań różniczkowych bądź różnicowych, zaś działania na nich są pełną analogią działań na tradycyjnych liczbach rzeczywistych (arytmetyka zmiennoprzecinkowa). Opisane niżej algorytmy są wykorzystywane przez autora do analizy obwodów elektrycznych skupionych i linii długich.