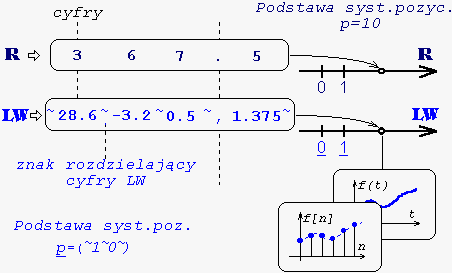
Liczby wielomianowe
to uogólnione liczby, które można używać do analizy stanów nieustalonych w układach podobnie jak liczby zespolone są używane do analizy stanu ustalonego przy wymuszeniu sinusoidalnym. Nadają się dobrze do analizy układów opisywanych niewymierną transmitancją w dziedzinie transformaty Laplace'a lub Z (np. linie długie).
Uogólnienie w przypadku liczby wielomianowej polega na tym, że jej cyfry są np. liczbami rzeczywistymi. Arytmetyka tych liczb bardzo przypomina arytmetykę zmiennoprzecinkową liczb rzeczywistych, z tą różnicą, że przy dodawaniu cyfr nie występuje przepełnienie. Stąd arytmetyka podstawowych działań jest taka sama jak arytmetyka wielomianów.
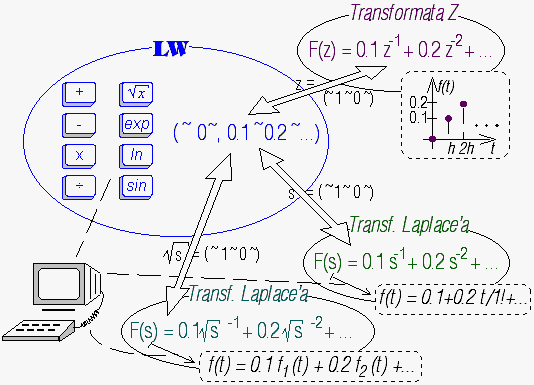Metoda liczb wielomianowych jest komputerowo wspomaganym rachunkiem operatorów - operacje, które wykonywałoby się wykorzystując transformaty Laplace'a czy Z na kartce papieru można wykonać całkowicie na komputerze wykorzystując tą metodę.